| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 커스텀 데이터 학습
- react native
- matplotlib
- yolo
- Expo
- STT
- skt fellowship 3기
- Loss Function
- google 로그인
- 코드업
- oauth
- C++
- google login
- 2021 제9회 문화공공데이터 활용경진대회
- YOLOv5
- google cloud
- marksense.ai
- @Transactional
- 졸프
- 순환참조
- AWS
- Spring
- html
- pandas
- 양방향 매핑
- javascript
- OG tag
- Spring Boot
- idToken
- JPA
- Today
- Total
민팽로그
[백준/BOJ] 11049: 행렬 곱셈 순서 본문
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
문제
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
- BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
입력
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
출력
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같다.
예제 입력
3
5 3
3 2
2 6예제 출력
90코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
int dp[501][501];
int main() {
int n;
cin >> n;
vector<pair<int, int>> v(n);
for (int i = 0; i < n; i++) {
cin >> v[i].first >> v[i].second;
}
for (int gap = 1; gap < n; gap++) {
for (int i = 0; i + gap < n; i++) {
int j = i + gap;
dp[i][j] = INT_MAX;
for (int k = i; k < j; k++) {
int res = v[i].first * v[k].second * v[j].second;
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + res);
}
}
}
cout << dp[0][n - 1];
return 0;
}
행렬의 곱셈 또한 연속하는 행렬끼리만 곱할 수 있기 때문에 11049: 파일 합치기 문제와 같다고 느껴서 쉽게 풀었다.
gap이 1일 때부터 n - 1일 때까지를 고려하며 dp[i][j]를 구한다. i와 j는 합칠 행렬의 구간을 나타낸다. 예를 들어 dp[2][4]는 2번 행렬부터 4번 행렬까지 곱했을 때 최소 연산 횟수를 의미한다.
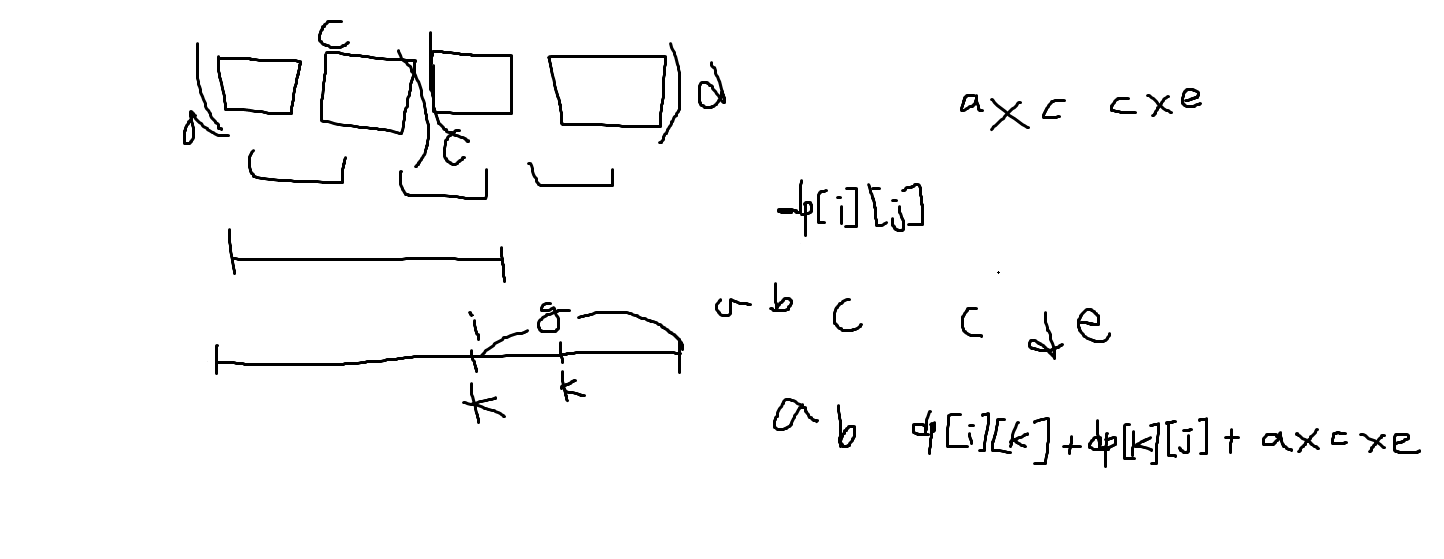
삼중 for문을 돌며 gap에 따라 i와 j 구간에서 최소가 되는 연산 횟수인 dp[i][j]를 구한다. i와 j 사이의 값 k를 이용하여 최솟값을 찾는다. dp[i][j]의 최솟값은 dp[i][j]와 dp[i][k] + dp[k + 1][j] + v[i].first * v[k].second * v[j].second 중 더 작은 값이 된다. 파란 부분은 구간 i부터 j까지의 행렬이 곱해지기 바로 직전까지의 최소 연산 횟수이고 초록 부분은 구간 i부터 j까지의 행렬을 합쳤을 때 새로 발생하는 연산 횟수이다.
마지막으로 0번 행렬부터 n-1번 행렬까지 모두 곱했을 때 dp값인 dp[0]d[n-1]을 출력한다.
'PS > 백준📖' 카테고리의 다른 글
| [백준/BOJ] 10942: 팰린드롬? (0) | 2022.03.01 |
|---|---|
| [백준/BOJ] 1520: 내리막 길 (0) | 2022.02.27 |
| [백준 / BOJ] 11066: 파일 합치기 (0) | 2022.02.27 |
| [백준/BOJ] 4803번: 트리 (0) | 2022.02.23 |
| [백준/BOJ] 5639: 이진 검색 트리 (0) | 2022.02.20 |

